matlab差分进化算法解决TSP问题

旅行商问题(Traveling salesman problem)，简称为TSP问题，是1959年提出的数学规划问题，TSP属于典型的NP完全问题；

TSP问题的语言描述：
在一个具有n个城市的完全图中，旅行者希望进行一次巡回旅行，或经历一次哈密顿回路，可以恰好访问每一个城市一次，并且最终回到出发城市。而这次巡回旅行的总费用为访问各个城市费用的总和，故旅行者同时希望整个行程的费用是最低的，求这个路线的排列策略？

TSP问题的实质可以抽象为：
在一个带权重的完全无向图中，找到一个权值总和最小的哈密顿回路
差分进化算法解决TSP问题的源码：DE解决TSP问题

代码如下：
 

%% 差分进化算法解决TSP问题，用最短的距离走完所有的城市（该怎样走？？？）
clc
clear
close all
F0=0.4;     %变异因子
CR=0.1;     %交叉概率
MaxGens=1000;
x_high=500;
x_low=-500;
X =[16.47,96.10
    16.47,94.44
    20.09,92.54
    22.39,93.37
    25.23,97.24
    22.00,96.05
    20.47,97.02
    17.20,96.29
    16.30,97.38
    14.05,98.12
    16.53,97.38
    21.52,95.59
    19.41,97.13
    20.09,92.55];
figure(1)
plot(X(:,1),X(:,2),'bo');
title('各个城市的分布情况')
% for i=1:length(X)
% text(X(i,1),X(i,2)+0.2,'a','color','k'); 
%  end
DM=Distanse(X);
D=length(X);
NP=8*D;
pop=rand(NP,D)*(x_high-x_low)+x_low; %初始化种群
g=1;        %迭代标记
fit=PathLength(DM,pop);
trace(1)=min(fit);
v=zeros(NP,D);      
for gen=1:MaxGens
    %%   变异操作
    for i=1:NP
        r1=randi([1,NP],1,1);
        pop_s = fit(r1);
        while(pop_s<fit(i))
            r1 =randi([1,NP],1,1);
            pop_s = fit(r1);
        end
        %% 产生r2,r3
        r2=randi([1,NP],1,1);
         while(r2==r1)||(r2==i)
            r2=randi([1,NP],1,1);
         end
        r3=randi([1,NP],1,1);
        while(r3==i)||(r3==r2)||(r3==r1)
            r3=randi([1,NP],1,1);
        end
        %% 交叉
        Z=randi([1,D],1,1);
        r=rand;
        for j = 1:D 
            if (r<=CR) || (j==Z)
                v(i,j)=(pop(r1,j)+pop(i,j))/2+F0*(pop(r1,j)-pop(i,j)+pop(r2,j)-pop(r3,j));
            else
                v(i,j)=pop(i,j);
            end
        end
        if PathLength(DM,v(i,:))<PathLength(DM,pop(i,:))
            pop(i,:)=v(i,:);
        end
    end
    %% 寻找出最优路径
    fit=PathLength(DM,pop);
    [trace(gen+1),d]=min(fit);
    tt=min(fit);
end
figure(2)
[~,pop(d,:)]=sort(pop(d,:),2,'ascend');
DrawPath(X,pop(d,:))
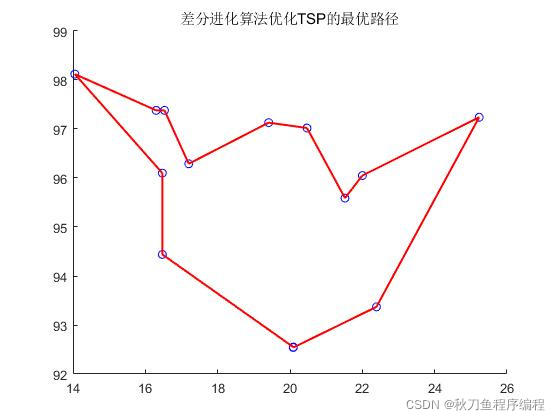
title('差分进化算法优化TSP的最优路径')
figure(3);
title('差分进化算法(DE), 最小值: ');
xlabel('迭代次数'); 
ylabel('目标函数值');
plot(trace);

最优路径连接（ DrawPath）：

%% 连接最优路径图
function DrawPath(a,R)
scatter(a(:,1),a(:,2),'bo');  %做算点图
hold on;
plot([a(R(1),1),a(R(length(R)),1)],[a(R(1),2),a(R(length(R)),2)],'r-','LineWidth',1.5);
hold on;
for i=2:length(R)
    x0=a(R(i-1),1);
    y0=a(R(i-1),2);
    x1=a(R(i),1);
    y1=a(R(i),2);
    xx=[x0,x1];
    yy=[y0,y1];
    plot(xx,yy,'r-','LineWidth',1.5);
    hold on;
end
end

输出结果（最短路径图）：